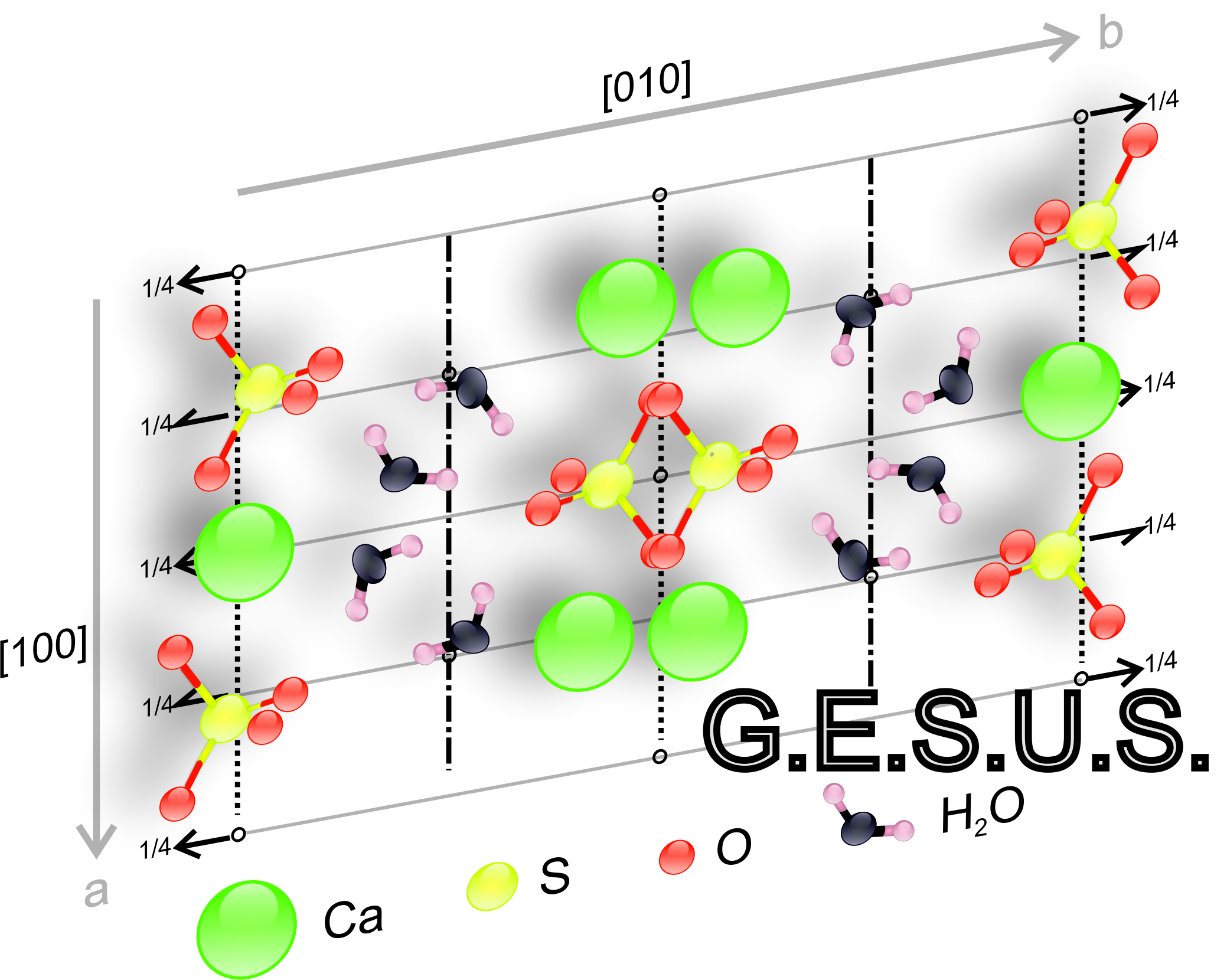
Lattice row: : A set of nodes connected by a translation vector, in a given direction. It can be defined by knowing the value of the translation vector "t ".
Lattice plane: A two-dimensional arrangement of nodes, defined by two non-parallel translation vectors and by the angle between them.
2D-lattice patterns (Bravais, 1866): Oblique "mp" (a≠b, α≠90°); rectangular "op" (a≠b, α=90°); centred rectangular "oc" (a≠b, α=90°, multiplicity=2); hexagonal "hp" (a=b, α=120°); and square "tp" (a=b, α=90°) (Fig. 4).
Fig. 4. 2D-lattice patterns.
2D-lattice centering: Only the rectangular lattice can be centred as "rectangular centered lattice".