Solving Space Groups with GESUS: Examples.

The software allows us to choose between 2 types of exercises:

• Deduce the symmetry operators from the arrangement of motifs (atoms) in a given cell (SG by general position).
• Deduce the symmetry operators from the notation of the Symmetry Space Group (SG by name).

---

• Open a file from the exercise library, e.g. 30.sgf

  A 4x4 rectangular lattice with two white atoms and two black atoms in different positions appear in the work window. The white ones have a "z" coordinate in the direction of "c", while the black ones are at z+1/2 (this coordinate is necessary since the drawing projected on the a, b plane does not allow its visualisation). The complete coordinates of the atoms are: x, y, z;   x,y+1/2,  z+1/2; x, y+1/2, z+1/2; x,y,  z.

  

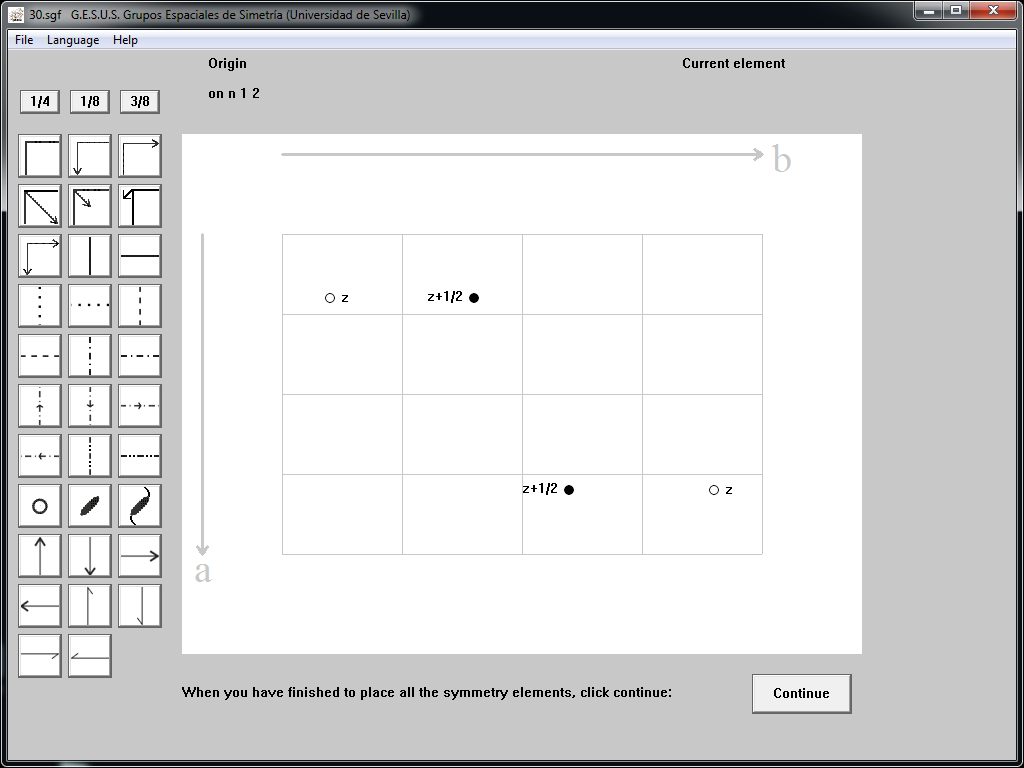
  Fig. 22.- Work interface of GESUS "Space Group by general posición"

  The software indicates that the origin is at n 1 2 so we can insert in the upper left corner of the grid (origin) a two-fold rotation axis parallel to "c" "2 [001]" and a glide plane "n" perpendicular to "a", i.e. "n (100)" (the identity is used to place the rest of the symbol's symmetry operators).

  Now, we can combine the binary with the perpendicular translations or see the relations between the motifs and place other twofold on the pattern.

  

  Fig. 23.- Combination of twofold at origin and perpendicular traslations"

  If we combine the glide plane "n in 0, y, z" with the perpendicular translation "a" we get another plane "n in 1/2, y, z".

  

  Fig. 24.- Combination of "a" translation and glide plane n(100)

  From the relationship between the first two atoms x, y, z; x, y,+1/2, z+1/2, we can deduce the existence of a glide plane "c in (0 1 0)" at 1/4, y, z from the origin. Combined with the perpendicular translation "b", another plane of type c is generated at 3/4, y, z from the origin which directly relates the other two atoms in the drawing.

  

  Fig. 25.- Combination of "b" translation and glide plane c(010)"

  The situation of displacement of 1/4 in the direction of "b" is caused by the presence of the glide plane "n" with translational components in b (it affects 1/4 in that direction for the twofold rotational axis at the origin) and in c (which does not affect it because it is parallel to that direction).

  

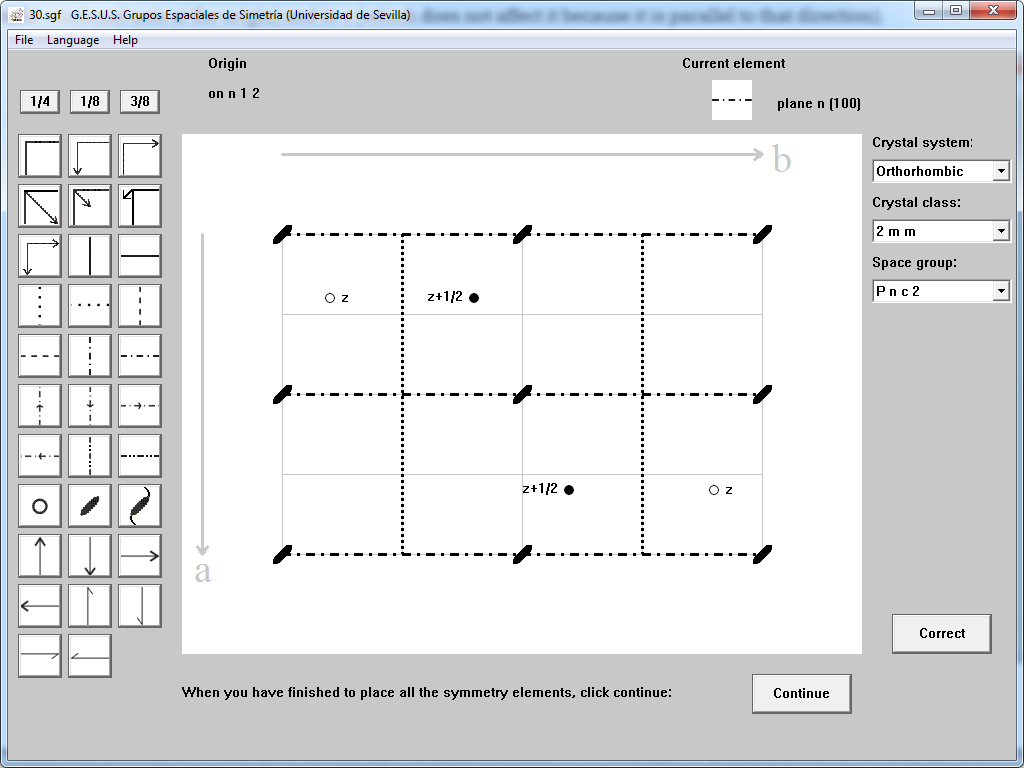
  Fig. 26.- Space Group nº 30 solved"

  As it has twofold axes parallel to "c" and glide planes type "n" perpendicular to "a" and type "c" perpendicular to "b", they are three axes of order 2, so the crystalline system would be orthorhombic, derived from the Point Group m m 2 and the notation of the Space Group would be P n c 2.