Space Groups of Symmetry
University of Seville (Spain)

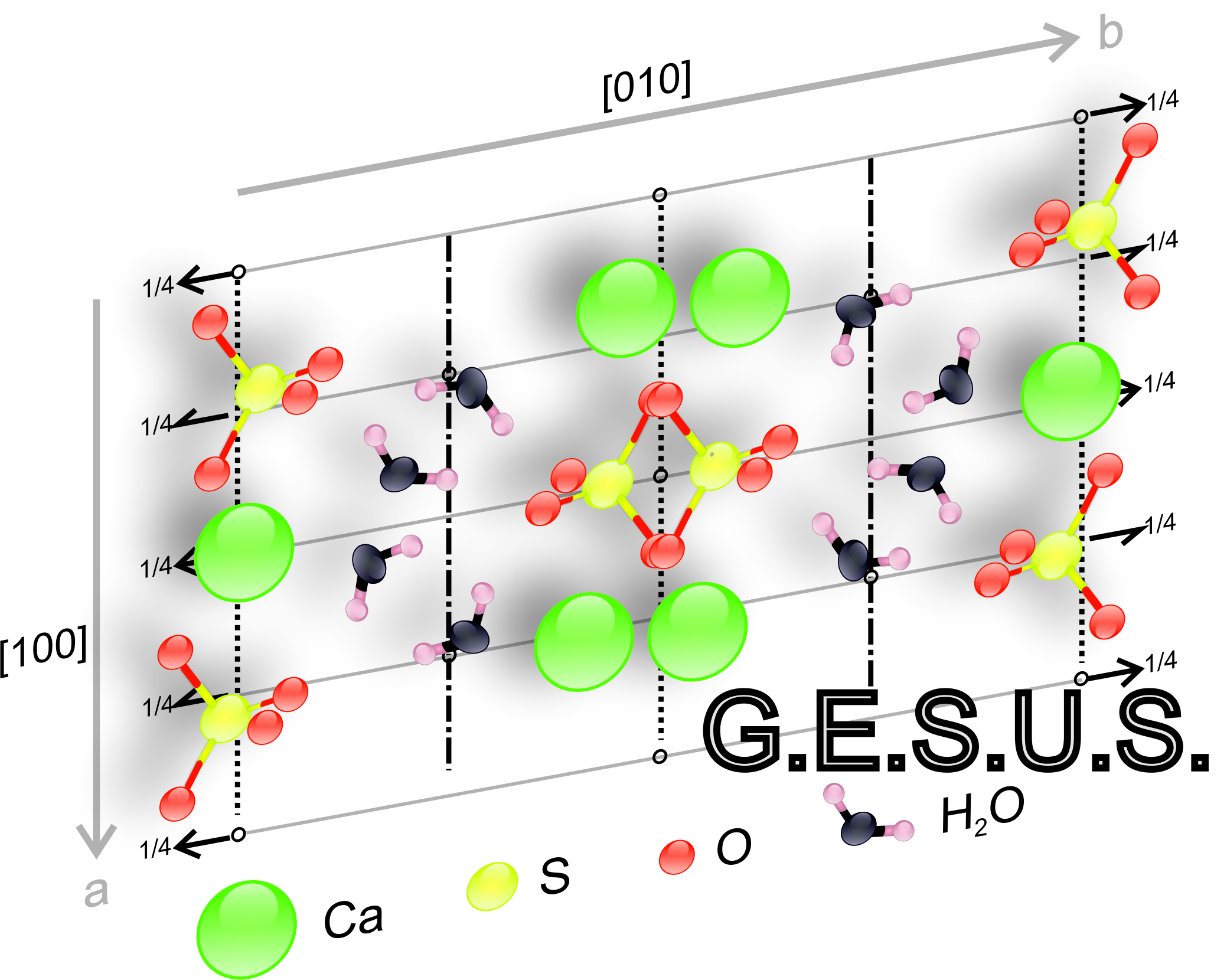
Symmetry operators: There are 5 general types of symmetry operators: translation, rotation axes (including identity), screw axes, rotoinversion axes (including the inversion centre and the reflection plane) and glide planes, which can be grouped in different ways:

Proper operators that generate homonymous or superimpose shapes (translation, rotation axes and screw axes).

Improper operators that generate enantiomorphic or opposite forms (rotoinversion axes and glide planes). These operators are called chiral and generate laterality (left and right) as occurs in the structures of proteins and nucleic acid molecules "biological groups".

Point symmetry operators: Axes of rotation, act upon all the points of the motif by rotating them by an angle α around an axis, whereby ∝=(360°)/N (where N "axis order" can only have values 1, 2, 3, 4 and 6 compatible with periodic patterns). The identity (monary axis) "1" is the neutral element or identity of the point groups, which makes any motif undistinguishable from any other motif.

Rotoinversion axes (1, 2, 3, 4   and 6 ) combine the rotation of all points of the motif by an angle ∝ around an axis of order N, with an inversion about a point at the centre of the axis (in space symmetry the point need not be at the centre of the axis). Certain operators of this type are considered special ("2  " is a reflection plane or mirror plane "m" and the rotoinversion operator "1  "  is a centre of symmetry).