Space Groups of Symmetry
University of Seville (Spain)

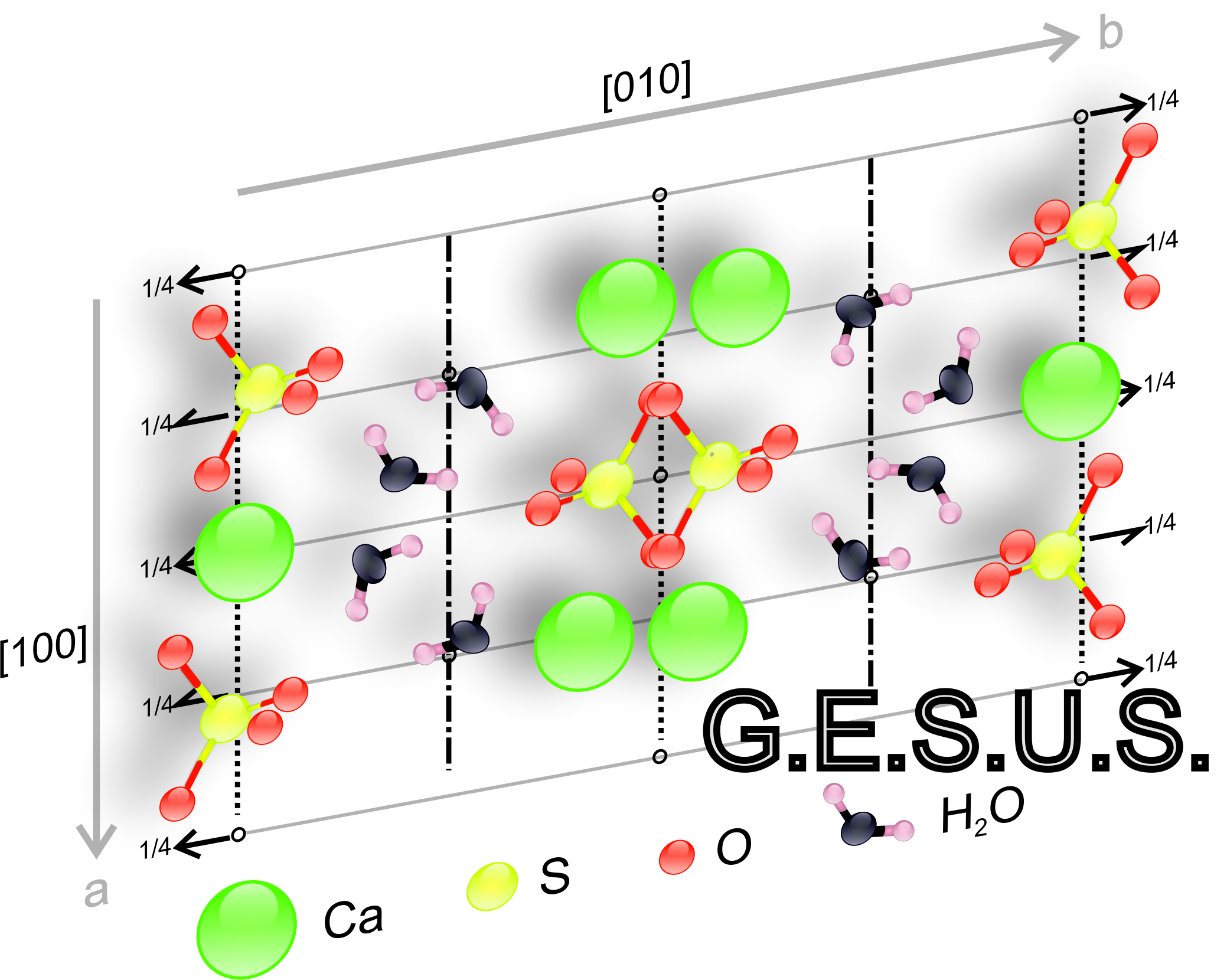
Symmetry Space Group Deduction: : Firstly, its general description must be interpreted and understood, for example: P 2/m 2/m 2/m

The first letter indicates the type of lattice (lower case if it is a Plane Group and capital letter for three-dimensional Space Symmetry Group).

The following three symbols indicate symmetry elements present in certain directions and also identify the crystalline system.

1.      Triclinic system: There are only axes of order 1 (identity or centre of symmetry).


2.      Monoclinic and Orthorhombic systems: The operators are arranged according to the directions of the reference system, in the order "a", "b", "c" (in the case of axes, parallel, and in the case of planes, perpendicular to these directions).
   The Monoclinic system only has operators in one direction, the other two are usually identity (e.g. A 1  1 2) and have at most 2 axes of order 2 (twofold and reflection/mirror plane).
   The Orthorhombic system has operators in all three directions and at least 3 axes of order 2 (twofold and/or reflection planes), e.g.: C c c 2.


3.      Tetragonal, Hexagonal and Trigonal systems: The order is now "c", "(a,b)", "bisector between a-b" (for axis are defined as parallel whereas planes are defined as perpendicular to these directions).
   The Tetragonal system has only one axis of order 4 which is placed parallel to "c" (fourfold rotation axis or fourfold inversion axis), e.g.: I 41/a 2/c 2/d, in this case, there is a fourfold screw axis parallel to "c" and a perpendicular mirror, two twofold axes parallel to "a" and "b" with glide planes type "c" perpendiculars and two other twofold axes on the bisectors of the crystallographic axes described above with other two perpendicular planes type "d".
   The Hexagonal system has a unique axis of order 6 which is arranged parallel to "c" (sixfold rotation axis or sixfold inversion axis), e.g. P 64 2 2, in this case, there is a sixfold screw axis parallel to "c"; three twofold axes parallel to "a", "b" and "i"; three other twofold axes on the bisectors of the crystallographic axes described above.
   The Trigonal system has only one axis of order 3 which is disposed of parallel to "c" (threefold rotation axis or threefold inversion axis), e.g. P3 m 1 (the identity is used to determine the location of the other operators), in this case, the threefold inversion axis parallel to "c" and reflection planes perpendicular to "a", "b" and "i".


4.      Cubic system: The order is now "(a, b, c)", "axes of order 3 at 54º44' from (a, b, c)", "bisector between a-b" (in the case of axes they are understood to be parallel, while in the case of planes they are understood to be perpendicular to these directions).
   The Cubic system is characterised by 4 axes of order 3 (ternary or inversion ternary) which are always placed in the central position of the Space Group symbol, e.g. F 41/d 3  2/c, in this case, there are 3 fourfold screw axes parallel to "a", "b" and "c" and 3 glide planes "d" perpendicular to them; 4 threefold inversion axes according to the diagonals of a supposed cube; 6 twofold rotation axes on the bisectors of the crystallographic axes and 6 glide planes "c" perpendicular to them.