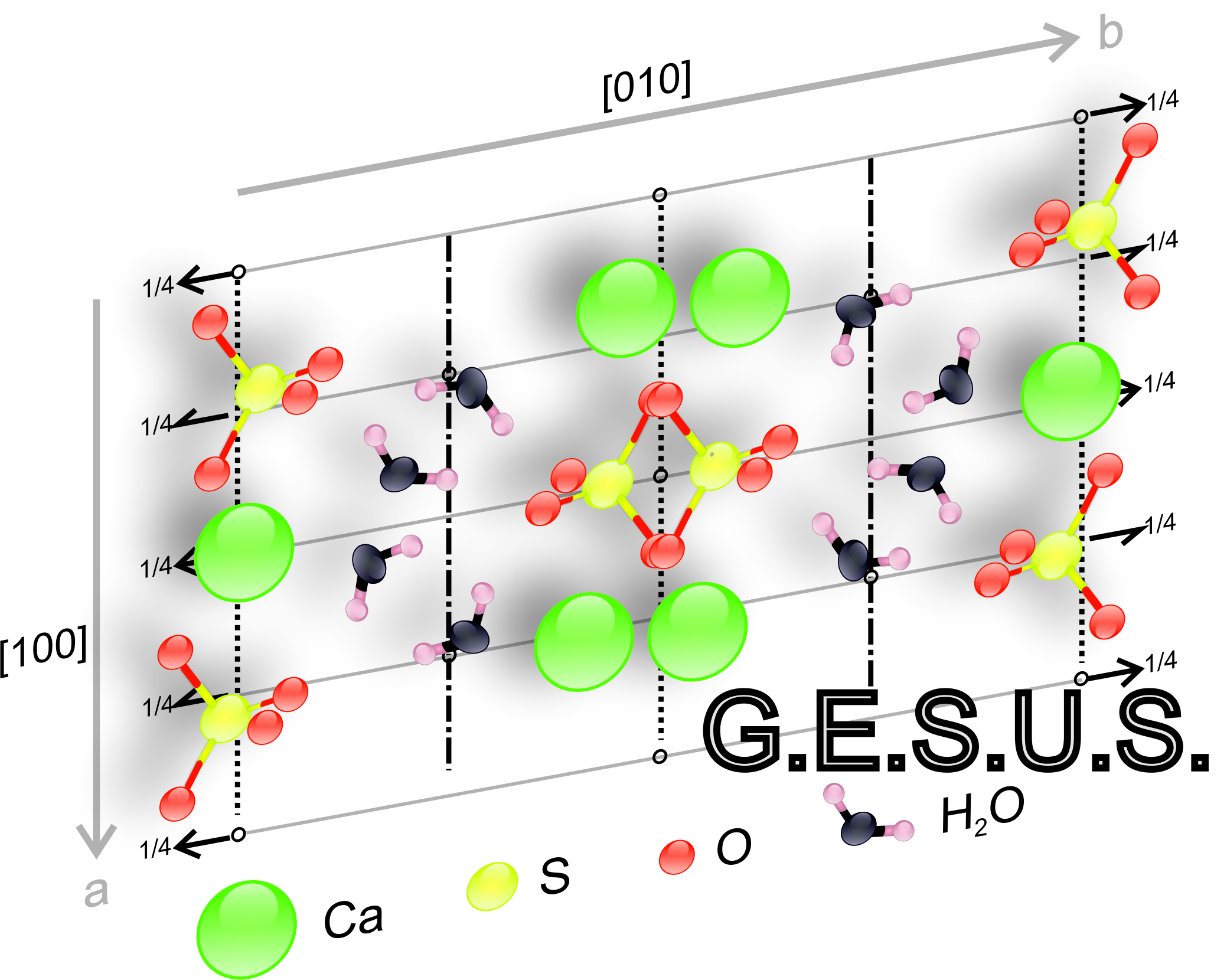
Symmetry operation "isometry": A transformation in three-dimensional space applied to an object or motif, which maintains the distances and angles and leaves the motif as a whole unchanged. If two symmetry operations are applied successively, the motif remains unchanged, so that the combination of these two operations is again a symmetry operation called "composition". Each symmetry operation can be undone by simply moving all the points of the motif back to their original position (inverse element). As the combination also contains the associative property and identity element, the set of isometries has the structure of a "mathematical group".
The isometries can be represented by transformation matrices of principal cosines, i.e. by unitary 3x3 square matrices |R|=±1 and orthogonal RT=R-1. The transformation matrix is then calculated by obtaining the cosines of the angles between the reference axes {O, a, b, c} of a Cartesian system and the new axes after performing the symmetry operation.
Fig. 8. Direction cosine matrix and reference basis vectors transformation
To find the new coordinates of a motif after a symmetry operation, the transformation matrix is multiplied by the original coordinates of the motif. X' = RX
If the transformation involves any translation, the corresponding translation vector is added: X' = RX + T
For example, XY reflection perpendicular to Z:
A twofold screw axis 21 parallel to "c":1