Symmetry Theory

Symmetry: Symmetry consists of several operations or processes by which an object "motif" can be led to match with others or with itself, in the same or different positions.

Point symmetry: Used to describe molecules and external crystal shapes, in general for periodic three-dimensional models in zero dimensions. 10 point-symmetry operators that are axes of rotation (proper and improper) and pass through a common invariant point that has zero dimension. A combination of these operators is possible, generating the 32 symmetry classes (point symmetry groups). As they do not contain translation, they apply to finite forms.

Linear symmetry: Used to describe one-directional periodic models (row group), in general for two-dimensional periodic models in one dimension. There are 7 one-dimensional groups including point symmetry operators (rotations of order 1 and 2) and glide planes (g).

Plane symmetry: Used to describe periodic two-dimensional models in two directions (mosaics). There are 17 two-dimensional "plane groups" including point symmetry operators (rotation 1, 2, 3, 3, 4 and 6, as well as reflection planes) and glide planes "g", all of which are perpendicular to the motif.

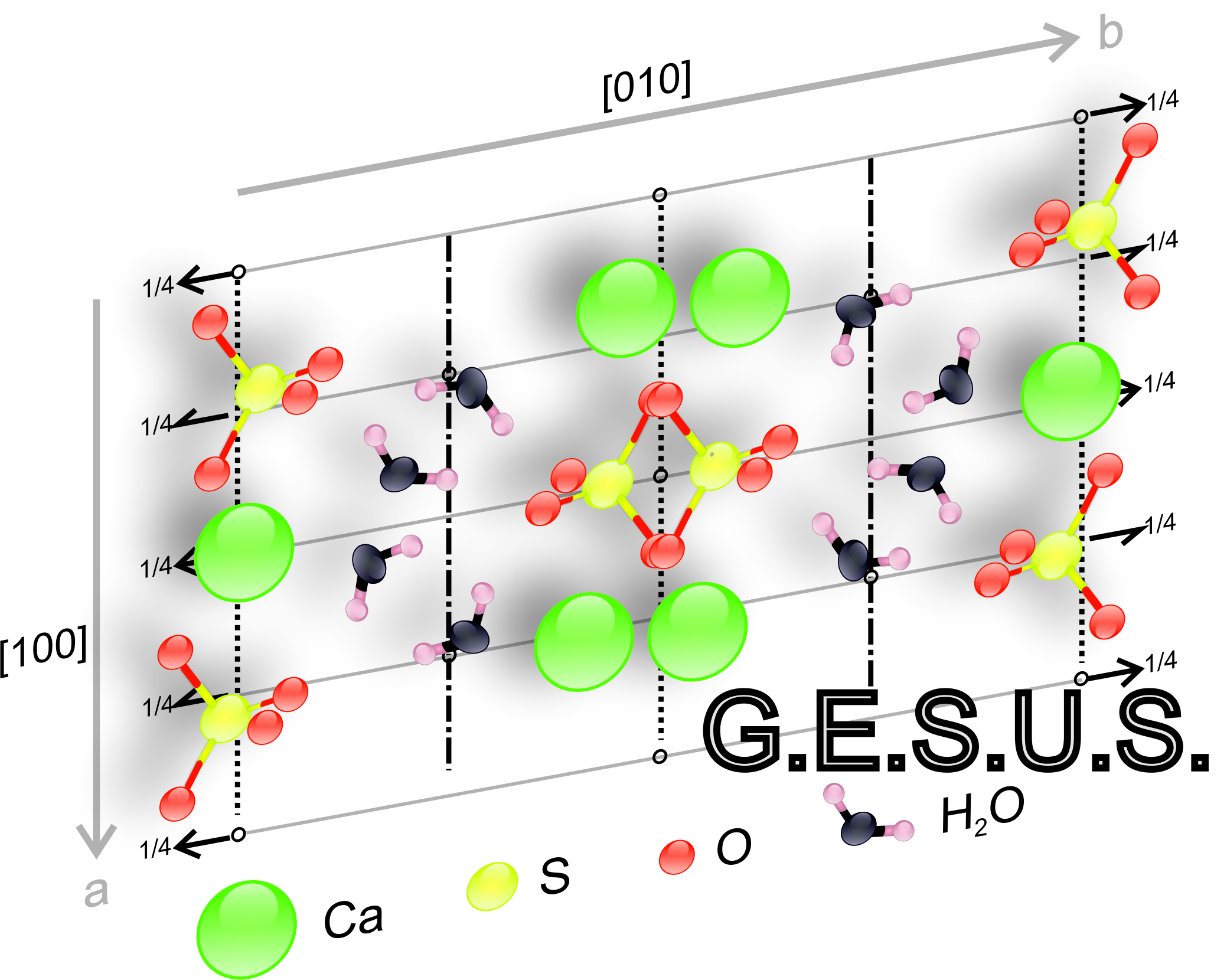
Space symmetry: Used to describe crystalline structures. The point symmetry elements and all their possible combinations with translations (screw axes and glide planes), generally describing periodic three-dimensional objects in three dimensions.

Systematization of crystal structures