Ejemplos de resolución de Grupos Espaciales con GESUS
- Deducir los operadores de simetría a partir de la disposición de motivos (átomos) en una celda dada (GES por posición general).
- Deducir los operadores de simetría a partir de la notación del Grupo Espacial de Simetría (GES por nombre).
- Abrimos un ejercicio de la biblioteca de ejercicios a partir de la opción "por motivos", p.e. 30.sgf
- Aparece en la ventana de trabajo un retículo rectangular 4x4 con dos átomos blancos y dos átomos negros en distintas posiciones. Los blancos poseen una coordenada “z” en la dirección de “c”, mientras que los negros están a z+1/2 (esta coordenada es necesaria puesto que el dibujo proyectado sobre el plano a, b no permite su visualización). Las coordenadas completas de los átomos son: x, y, z; x,+1/2, z+1/2; , y+1/2, z+1/2; ,, z.
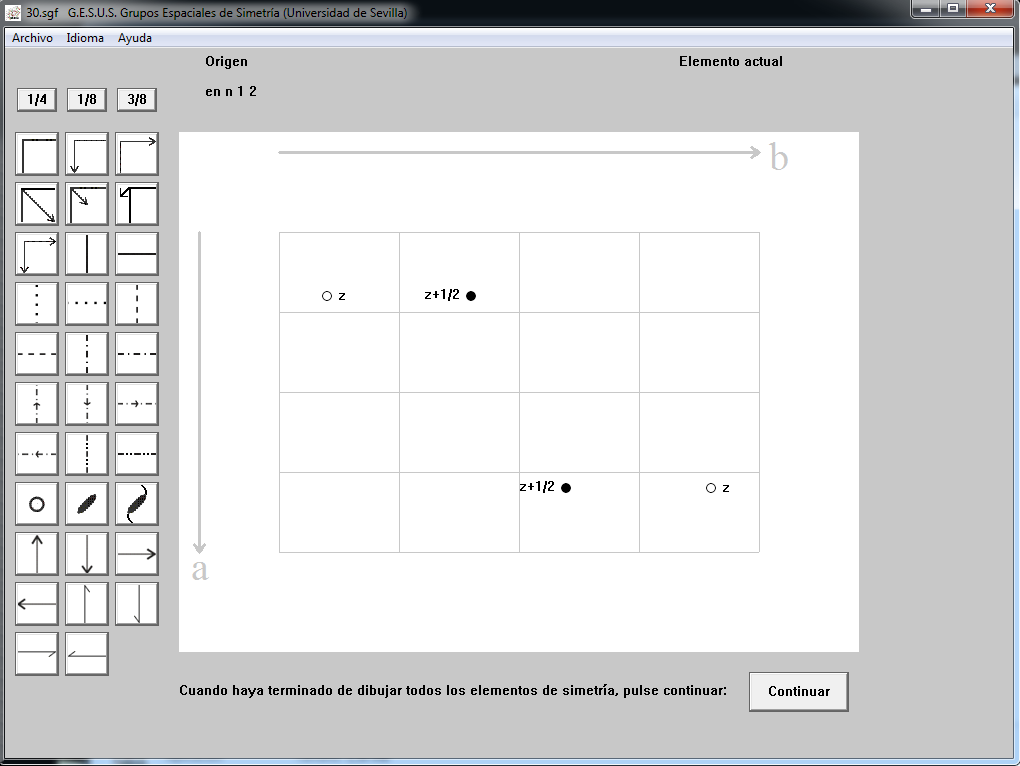
Fig. 22.- Ventana de trabajo "GES posición general"
El programa nos indica que el origen está en n 1 2 con lo que podemos colocar en la esquina superior izquierda de la cuadrícula (origen) un binario paralelo a “c”, es decir 2 [001] y un plano de deslizamiento “n” perpendicular a “a”, es decir n (100) (el monario sirve para situar el resto de operadores de simetría del símbolo).
Ahora podemos realizar la combinación del binario con las traslaciones perpendiculares o ver las relaciones entre los motivos y colocamos otros binarios sobre el dibujo.
Fig. 23.- Actuación de vectores perpendiculares sobre el binario en origen"
Si combinamos el plano de deslizamiento “n" en 0, y, z con la traslación perpendicular “a” obtenemos otro plano “n" en 1/2, y, z.
Fig. 24.- Actuación del vector "a" sobre el plano n(100)
Si nos fijamos en la relación existente entre los dos primeros átomos en posiciones x, y, z; x,,+1/2, z+1/2, se deduce la existencia de un plano de deslizamiento “c" en (0 1 0) a 1/4, y, z del origen. Si combinamos con la traslación perpendicular “b”, se genera otro plano de tipo "c" a 3/4, y, z del origen que relaciona directamente a los otros dos átomos del dibujo.
Fig. 25.- Actuación del vector "b" sobre el plano c(010)"
La situación de desplazamiento de 1/4 en la dirección de “b” está ocasionada por la presencia del plano n con componente traslacional en "b" (afecta 1/4 en dicha dirección respecto al binario en origen) y en c (que no le afecta por ser paralelo a dicha dirección).
Una vez colocados todos los elementos de simetría que relacionan las posiciones atómicas en el dibujo, pulsamos continuar y se nos preguntará por el sistema, por el Grupo Puntual compatible y por el Grupo Espacial a que corresponde.
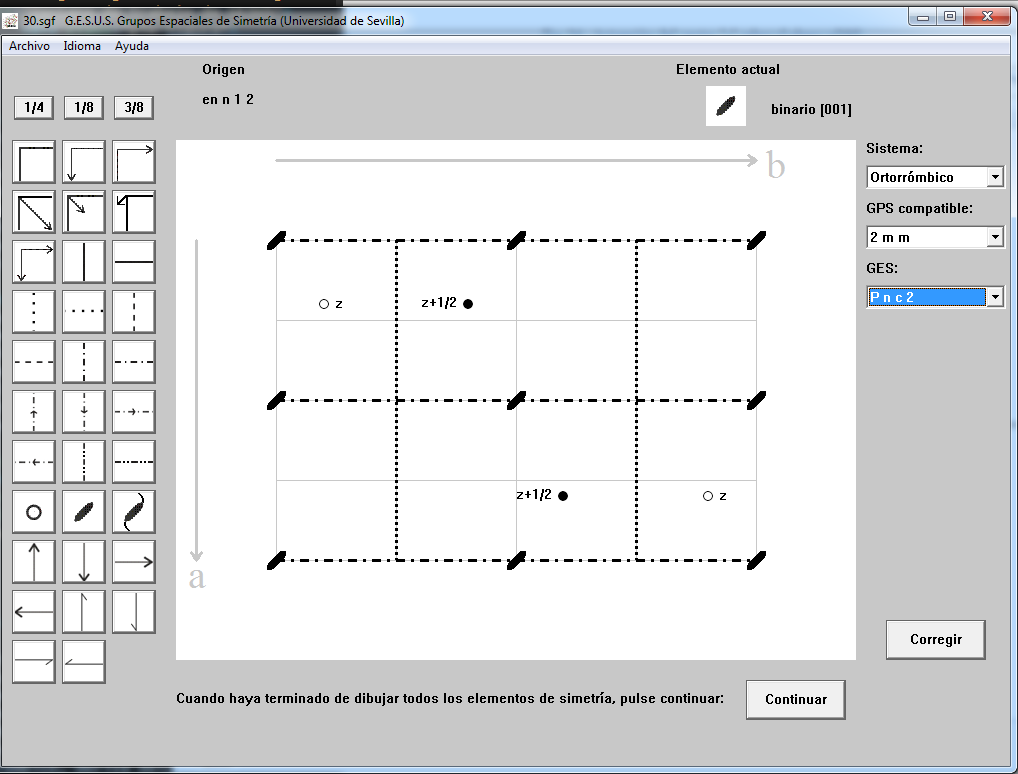
Fig. 26.- Grupo espacial nº 30 resuelto"
Como tiene binarios paralelos a “c” y planos de deslizamiento tipo “n” perpendiculares a “a” y planos de tipo “c” perpendiculares a “b”, son tres ejes de orden 2 (1 binario y 2 planos) en las tres orientaciones de los vectores del sistema, por lo que el sistema cristalino sería ortorrómbico, deriva del Grupo Puntual m m 2 y la notación del Grupo Espacial sería P n c 2.