Teoría de Simetría

Simetría: Consiste en una serie de operaciones o procedimientos por los que un objeto "motivo" se puede llevar a coincidir con otros o consigo mismo, en la misma o en distintas posiciones.

Simetría puntual: Se utiliza para describir moléculas y formas externas de cristales, en general para modelos tridimensionales periódicos en cero dimensiones. Hay 10 operadores de simetría puntual que son ejes de rotación (propios e impropios) y pasan por un punto común invariante que tiene dimensión cero. Es posible la combinación de estos operadores, generando las 32 clases de simetría (grupos puntuales). Como no contienen traslación se aplican a las formas finitas (moléculas, formas poliédricas externas de los cristales).

Simetría lineal: Se utiliza para describir modelos periódicos en una sola dirección (cenefas), en general para modelos bidimensionales periódicos en una dimensión. Hay 7 grupos unidimensionales que incluyen operadores de simetría puntual (rotaciones de orden 1 y 2) y planos de deslizamiento (g).

Simetría plana: Se utiliza para describir modelos bidimensionales periódicos en dos direcciones (mosaicos). Hay 17 grupos bidimensionales "grupos planos" que incluyen operadores de simetría puntual (rotaciones propias 1, 2, 3, 4 y 6, así como planos de reflexión) y planos de deslizamiento "g", todos ellos perpendiculares al motivo.

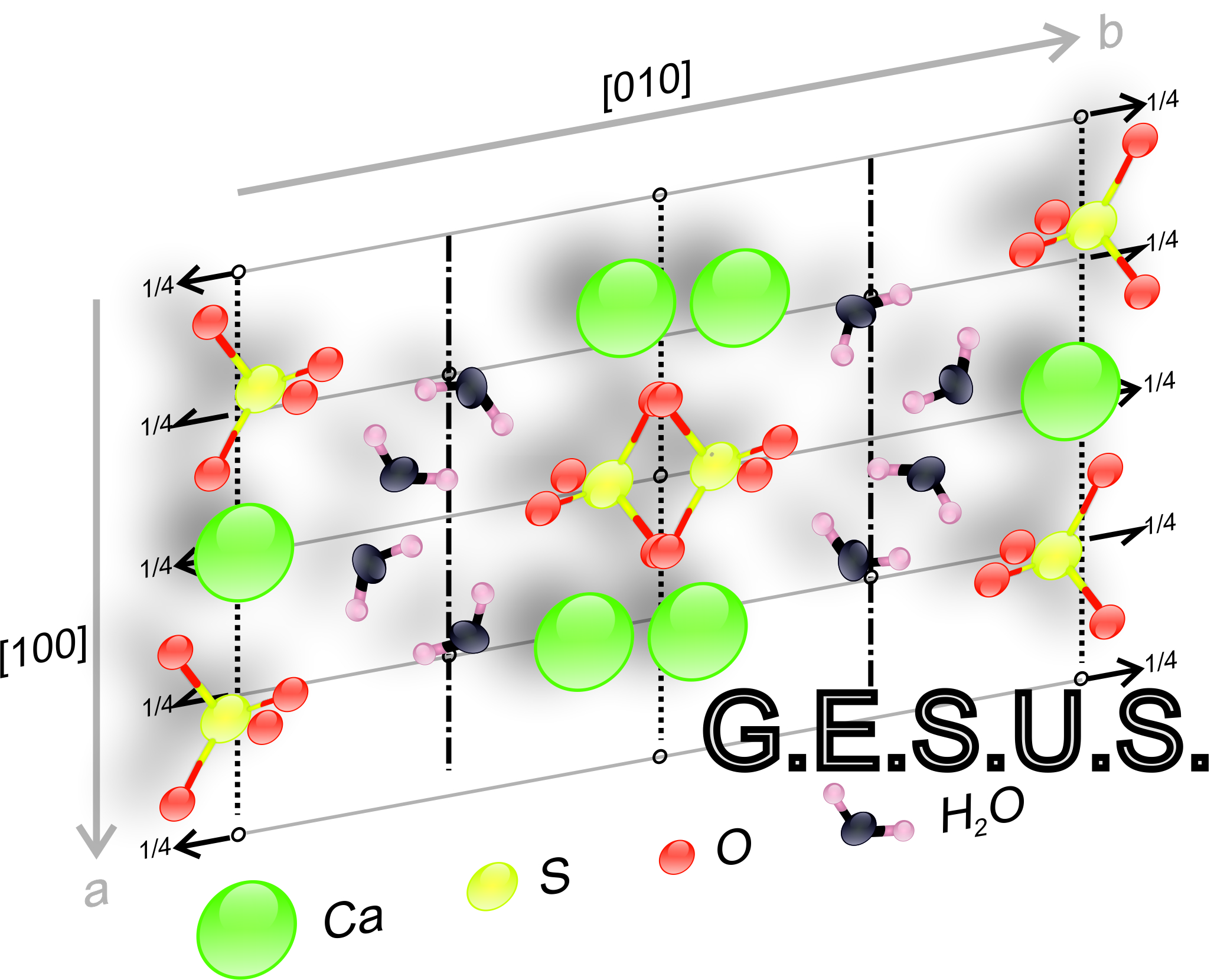
Simetría espacial: Se utiliza para describir estructuras cristalinas. Hay 230 Grupos Espaciales de Simetría que operan con los elementos de simetría puntual y todas sus posibles combinaciones con traslaciones (ejes helicoidales y planos de deslizamiento), en general describen objetos tridimensionales periódicos en tres dimensiones.

Sistematización de las estructuras cristalinas